(ICRA2020)Unigrasp
UniGrasp的出现确实让人耳目一新,感觉sequential地出n指灵巧手的抓点确实是一个很符合逻辑很直观的想法。并且这个工作比起6D-GraspNet和GraspNet-1Billion,有尝试对Gripper的URDF建模,也就是关注了夹爪的动力学模型,而之前的6D-GraspNet虽然在第二步的Grasp Pose Evaluation中,把夹爪的点云接在了原先待抓取点云之后,但是这其实更多的是对夹爪静态几何特征的提取。虽然对URDF建模的方法,我个人的直觉一定不是最优解,比较naive,但是也算提出了一个方向。
首先,这篇文章主打的就是把gripper的attributes(几何、动力学)和待抓取物体的feature联合作为Input输入,然后通过一个变长stage的方法来输入自定义自由度的机械爪的抓点。
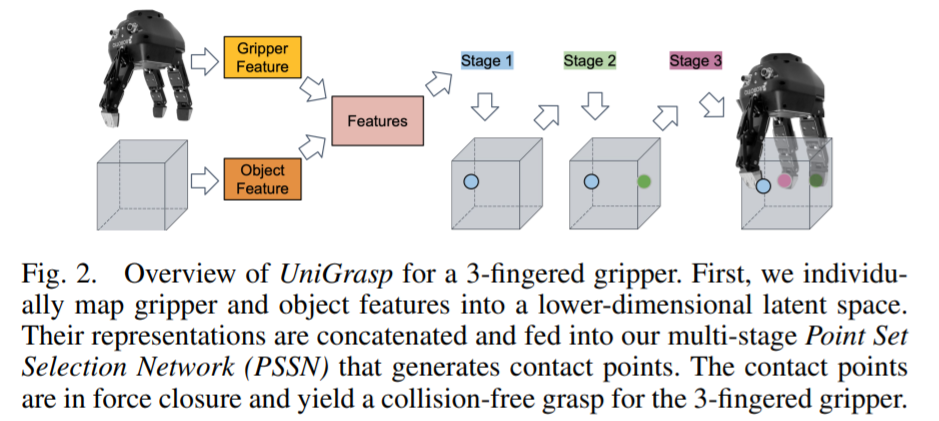
正如文中所说,最终网络的输出的n个点,必须满足两个条件:force-closure和reachable(ik可解)。其实稍微检索一下就可以知道,在传统机器人领域,灵巧手的抓取判定条件,包括传统ik,都是基本上30年前研究完成的问题。感叹一下机器学习真的就是大一统了,可以把几十年前分析完毕的领域拿过来作为训练集正样本条件来做data-driven。
对Gripper的建模
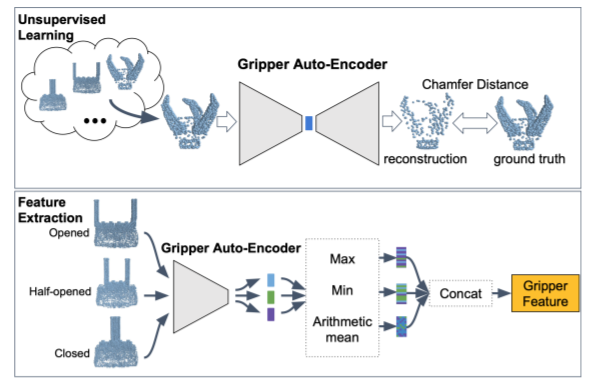
基本上就是拿Gripper先训了一个AE,然后拿AE的Encoder部分来提夹爪的特征。注意到,上图是以2-fingered gripper为例的,它需要通过URDF构建出全开、全闭、半开三个点云喂入,得到3个特征向量,然后做max, min, mean-pooling最终得到3个特征向量输入。对于一个n-DOF gripper,它需要对每个自由度都枚举一遍最大和最小,然后再加上所有自由度的中值作为额外的一个点云,也就是$2^N+1$个点云输入,后面的3个pooling保证了所有输出的维度相同。
我认为这对于纯单个关节驱动的手指还好,如果是多节的那种灵巧手,这相当于尝试用一个神经网络去解IK问题,可能这种取最大值和最小值的输入是不够对整个动力学系统建模的。我看了看Intel做的求解IK的神经网络,其中的数据收集就是对游戏角色做大量的随机Pose的ik采样来创建数据,包括说用RL做的。考虑到这里不仅仅是IK的问题,更多意义上还有必须要和待抓取物体collision-free的因素,所以这个问题还是挺tricky的。
因为这篇论文的野心很大,希望通过这样的Gripper-Encoding的方式来泛化到所有的Gripper,根据上文中的分析显然是很难以做到的,所以其实我们在最终它的实验中也可以发现,它只做了一个unseen 2-fingered gripper的对照组,没有做多指的情况。包括说它虽然整个框架说支持n指,实际上也只做了2指和3指的,因为收集数据的难度和训练成功率都是会有很明显的影响的。
PSSN
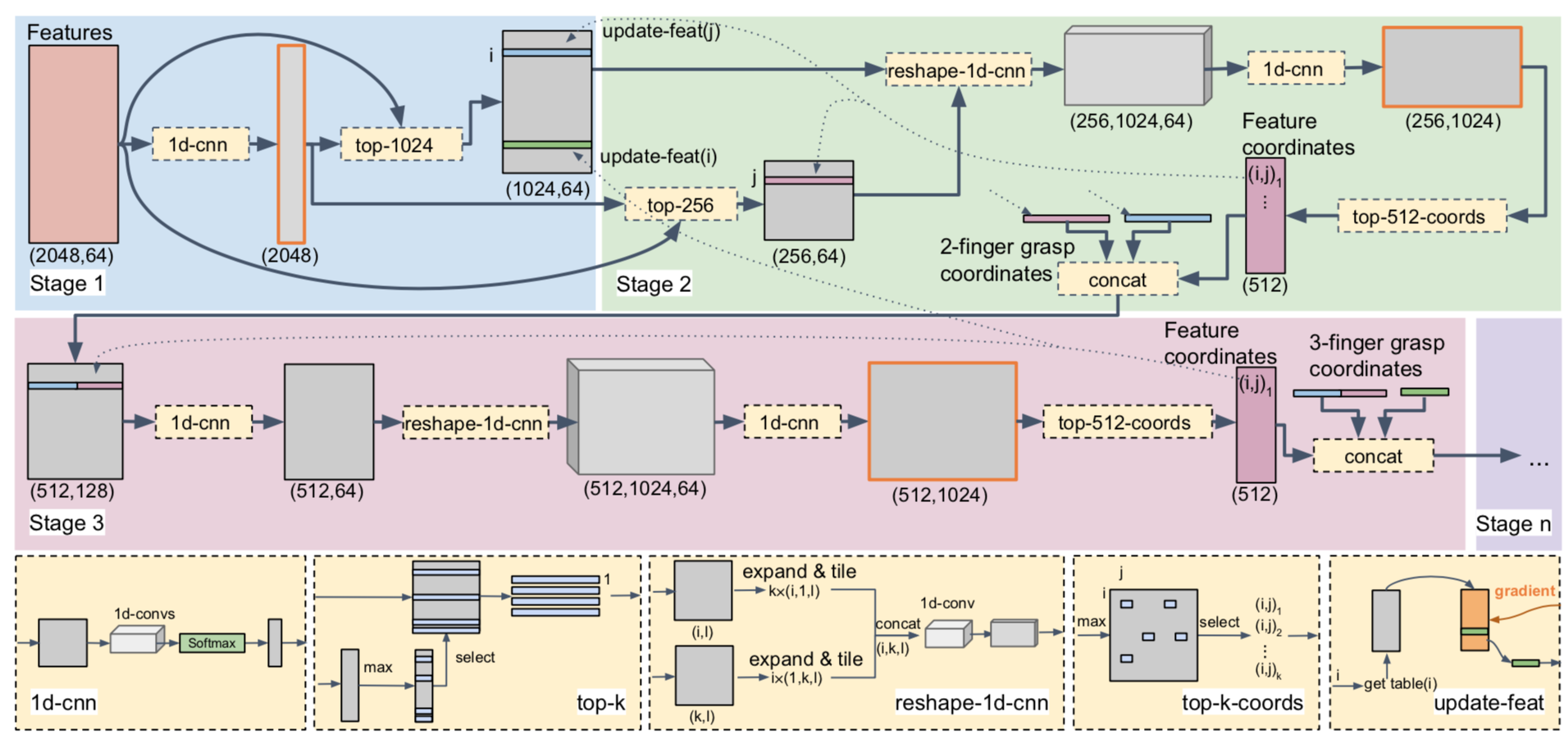
第一阶段
原先的点云:
- $S_0={p_i}_{i=1}^L$, $F_0 : (L, 64)$
首先我们对$F_0$做1D CNN,得到$(L, 1)$,然后对这$L$维做一个softmax,得到每一个点的合法的概率(probability of each point being valid)。然后按照score从高到低选出$K_1$个点以及对应的特征。
第二阶段
此时我们拥有的数据如下
$S_0={p_i}_{i=1}^L$, $F_0 : (L, 64)$
$S_1={p_i}_{i=1}^{K_1}$, $F_1 : (K_1, 64)$
第二阶段和第一阶段类似,我们仍然需要从$S_0$中选出$K_2$个点,即我们得到了$S_2={p_i}_{i=1}^{K_2}$, $F_2 : (K_2, 64)$。接下来,我们要把$F_1$和$F_2$组合起来,得到最先2个抓点的预测。论文中提到的是做了一个reshape-1d-cnn得到了$F_3 : (K_2, K_1, 64)$,具体流程如下图所示:
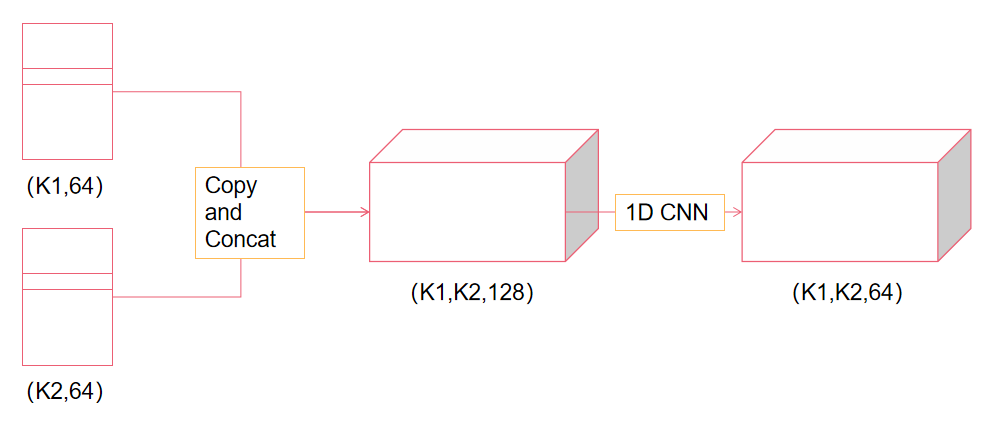
然后我们继续用1d-CNN从$F_3$得到$(K_2,K_1, 1)$,作为每个点对的分数,我们从中选出$K_3$个分数最高的点对,记为$S_3$。对于二指夹爪的情况,PSSN到此为止就结束了。
第三阶段
在这个阶段中,网络需要继续预测出第三个接触点。网络需要继续从$S_3={p_i,p_j}_{i=1,j=1}^{K_2,K_1}$中提取特征,$S_3$中的每个元素代表着从Stage1和Stage2中选择出的两个点。我们把对应的点对的特征连在一起,得到了$(K_3,128)$,继续做1D-CNN得到$F_4 : (K_3,64)$。我们继续把$F_1 : (K_1,64)$拿过来和$F_4$做reshape-1D-CNN,我们可以得到$F_5 : (K_3, K_1, 64)$,再1D-CNN + softmax得到大小为$(K_3,K_1)$的分数矩阵。其中在$(u, v)$处的值代表着$S_3$的第u个点对和$S_4$中的第v个点组合起来的分数。根据这一点,我们可以从中选出TOP-$K_4$的contact point三元组集合。这就是三指的情况。
在实际训练中,我们发现训练PSSN来reject大量不合法的点的集合是更容易的。如下的启发式算法把十亿的三元组抓点集合减少到了百万的数量级。首先,PSSN预测点云的法向量,我们把预测出来的法向量的集合记为${\hat{pn_i}}_{i=1}^L$。然后,我们利用简单的启发式算法来根据点的位置和对应的法向量来reject不合法的点的集合。
- 对于二指机械手的情况,两个接触点的法向量需要大于120度来满足force-closure
- 对于三指机械手的情况,三个接触点需要构成一个三角形,并且我们约束三角形的每一边都要大于1cm,以免选出来的点太近了,并且为了让三角形更加常规一点,额外约束三角形的最大角不超过120度,对于每个接触点,它的法向量和两条边的角度小于90度(也就是让法向量朝三角形的外部指)。总而言之,三指的force-closure会满足上述的约束。
Loss
对于法向量的预测,Loss如下所示:
$$
L_{pn}=-\sum_{i=1}^L(\hat{pn_i}\cdot pn_i)
$$
对于一个物体的点云和夹爪,我们把满足force-closure和夹爪可达的点集标为正例,其余的点集标为负例。因此,每个点集都会有一个二分类标签$y$。对于第n个阶段,网络预测出一系列的点集$K_n$,以及对应的标签$\hat{y}$标志着点集的valid概率。基于这些预测概率,我们可以得到这些点的集合的一个排好序的列表。我们使用ListNet损失来提升正例所对应的$\hat{y}$
$$
L_n=-\sum_{j=1}^{K_n}y_ilog\left(\frac{\text{exp}(\hat{y_j})}{\sum_{j=1}^{K_n}\text{exp}(\hat{y_j})}\right)
$$
在训练过程中,我们先训练Stage 1,我们只计算Stage 1的Loss,但是梯度也会修改Stage2的参数。在Stage 1训练完之后,我们固定Stage 1的参数来继续训练Stage 2,此时只计算 Stage 2的Loss。这个步骤反复执行,直到训练到 Stage N。
数据收集
在仿真环境中,选出了1000个物体模型,并且按照5个大小来scale,最终得到3275个物体。使用12种不同的机械手,9个是二指的,3个是三指的。
把物体放在水平面上,通过八个角度的摄像头来创建深度图,并且合成一个点云并且降采样到2048个点。给定一个N指的机械手,我们需要创建出N个点所有的可能的contact point set,其需要满足force-closure和reachable。
在2048个点和三指的情况下,有$C_{2048}^3 \approx 1.4\times10^9$种可能性。我们假设二指的摩擦系数为0.5,三指的摩擦系数为0.65,并且使用16面的多边形对摩擦锥近似,并且使用之前提到的启发式算法来拒绝大量的point sets。我们使用FastGrasp来评估点的集合,并且计算Grasp质量的分数$Q_l^-$。
- 对于二指,$Q_l^->0$认为满足force-closure。
- 对于三指,$Q_l^->0.0001$认为满足force-closure。
对于满足force-closure的点的集合,我们使用N指机械手的ik来计算其可达性,需要满足以下两个条件:
- reachable,ik可解。
- 和物体的点云没有碰撞,collision-free。
只有force-closure、reachable、collision-free三个条件全部满足,我们才会标注为positive。
(ICRA2020)Unigrasp