(ICCV2021)A-SDF

​ 最近的工作有很多利用implicit function来做3D刚体重建，但是很少工作关注通用关节体的建模，比起刚体，关节体的自由度更大，所以泛化到未见过的形状比较困难。为了解决形状的方差较大的问题，这篇文章引入了 Articulated Signed Distance Functions (A-SDF) 来使用隐空间来表示关节体的形状。我们假设没有对关节体部分的几何信息、关节类型、关节轴、关节位置的先验知识。

问题重述

​ 我们考虑在一个关节体类别上的N个模型实例。每个实例都会有M个位形，这样我们就有了$N \times M$个形状。我们令$\chi_{n,m}$代表了第n个实例的第m个位姿的形状，其中$n\in\{1,…,N\},m\in\{1,…,M\}$。每个形状$\chi_{n,m}$会有一个形状编码$\phi_n\in R^C$和关节编码$\psi_m\in R^D$，其中$C$代表了隐变量空间的维度、$D$代表了关节体的自由度。

形状编码

​ 形状编码$\phi_n$是在同一个关节体实例中共享的，也就是不同位姿有相同的形状编码。在训练过程中，我们对于每个实例维护并更新形状编码。

关节编码

​ 我们使用关节角度来作为关节编码。比如说，2D的关节体（如：眼镜）且两个关节均打开45度的关节编码为$\psi_m=(45^{\circ},45^{\circ})$，关节角度定义为物体标准位形的相对角度。

网络

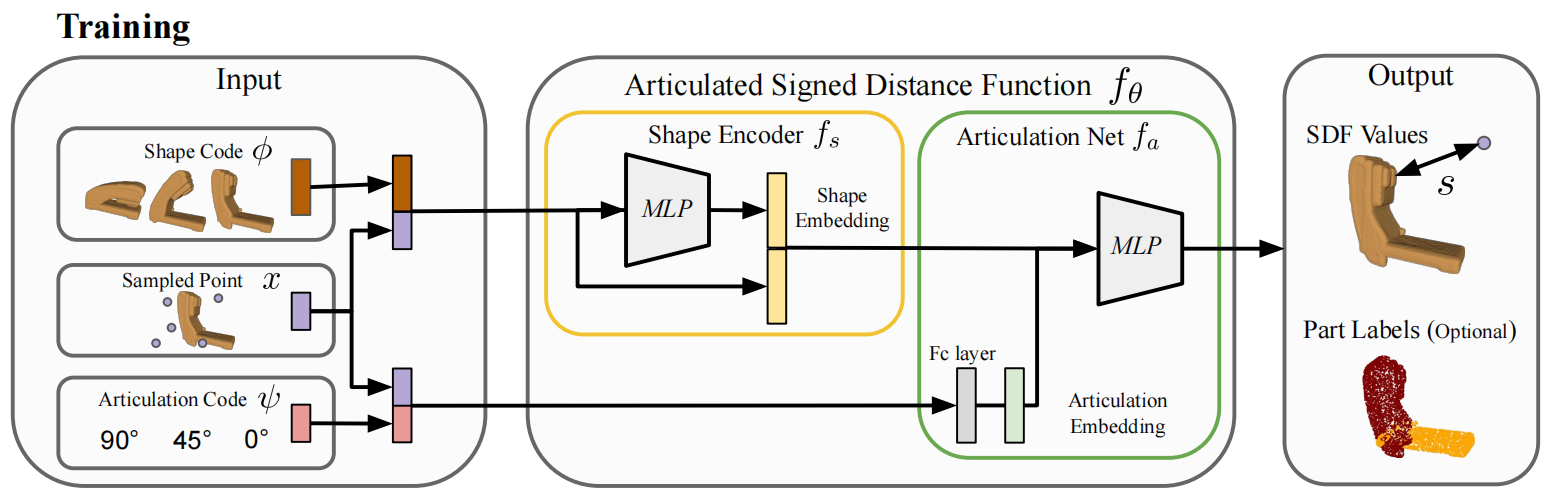
​ 如上图所示，A-SDF函数$f_{\theta}$最终定义如下：
$$
f_{\theta}(x,\phi,\psi)=f_a[f_s(x,\phi),x,\psi]=s
$$
​ 其中$f_s$是shape encoder，而$f_a$是articulation network，$\textbf{x}\in R^3$为形状中采样到的点，$s\in R$是标量SDF函数了，SDF函数值的正负描述了是在物体外（正）还是物体内（负）。并且SDF函数等于0的等值面$f_{\theta}(\cdot)=0$隐式地描述了3D形状。SDF也就是有向距离场，之前的文章中也遇到过。

​ 自此，其实我们就可以知道S这个网络就是用2个我们提的形状编码和关节编码，以及多个点的query来回归出整个SDF函数。并且当我们的网络训练完成，且我们通过某些办法得到了形状编码以后，我们就可以传入未训练过的关节值来得到合成的3D模型，也就是SDF函数场。这样看来SDF函数虽然是十年前就有的东西，但是借助着implicit function的东风，learning界重新发现了它可以3D模型建立映射关系，并且嵌入到网络中。

​ 但是，形状编码它对于同一个关节体实例是共享的，所以它要在某种意义上能够描述出关节体的动力学模型，这样它才能够为我们infer unseen joints提供帮助。我认为这个相对困难，在下文中我将继续尝试探索它的隐变量空间的参数是怎么训练的。

训练过程

​ 在训练过程中，给定GT关节编码$\psi$，从形状中采样的点以及对应的SDF值，我们希望训练模型来优化形状编码和模型参数$\theta$。网络的真正逻辑如下图所示，论文中的图的逻辑相对模糊一些。

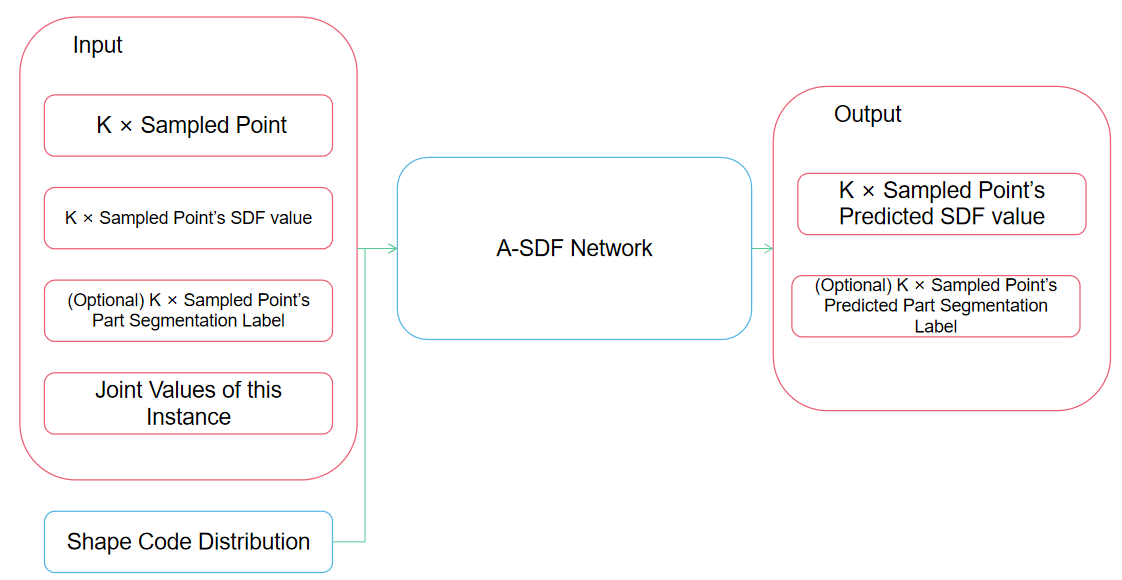
​ 那无非接下来就是去学这个网络的参数，我们使用如下的损失函数：
$$
L(\chi,\phi,\psi)=L^s(\chi,\phi,\psi)+\lambda_pL^p(\chi,\phi,\psi)+\lambda_{\phi}||\phi||_2^2 \\
L^s(\chi,\phi,\psi)=\frac{1}{K}\sum_{k=1}^K||f_{\theta}(x_k,\phi,\psi)-s_k||_1 \\
L^p(\chi,\phi,\psi)=\frac{1}{K}\sum_{k=1}^K[CE(f_{\theta}(x_k,\phi,\psi),p_k)]
$$
​ 其中$L^s$就是逐点地去回归这个SDF函数，而$L^p$就是如果我们要同时预测关节体分割网络的话，对应的逐点的分类交叉熵损失，而第三部分的$\lambda_{\phi}||\phi||_2^2$就是对我们的形状参数的正则化约束。

​ 在训练过程中，形状编码最初初始化为正态分布，后面我们是要持续更新它的，因为它是在$N \times M$个训练样本中共享的，所以它和网络参数$\theta$是要一起训练的，也就是：
$$
\theta^*,\phi_n=\arg\min_{\theta,\phi_n}\sum_{n=1}^N\sum_{m=1}^ML(\chi_{n,m},\phi_n,\psi_m)
$$

应用

​ 这个工作的应用阶段比较有意思，对我来说比较崭新。

Basic Inference

​ 给定一个关节体模型$\chi$，我们现在的目标是恢复出对应的形状参数$\phi$和关节角度$\psi$。

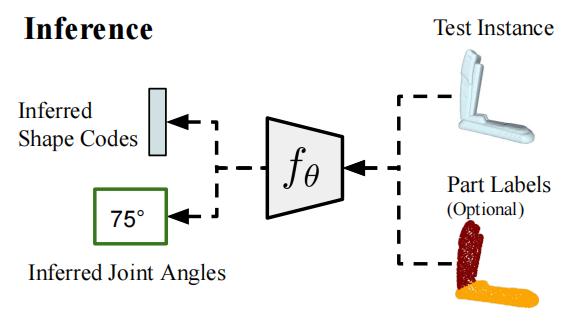
我们可以在原先网络上使用反向传播来求得。也就是我们固定网络参数，然后随机初始化两个待求目标$\phi,\psi$。然后我们通过优化如下目标来求得最优情况：
$$
\hat{\phi},\hat{\psi}=\arg\min_{\phi,\psi} L(\chi,\phi,\psi)
$$
​ 但是注意到待求问题无论是$\phi$和$\psi$都是非凸的，基于梯度的方法可能会导致到达局部最优的情况。在实际运用过程中，我们发现直接通过梯度来估计关节角度可以收敛到一个比较好的结果，但形状参数不行。所以我们先估计出关节角度，然后在固定关节角度和网络参数的情况下，再对形状参数做优化。

TTA(Test-Time Adapation Inference)

​ 上述的Basic Inference的准确度极大地依赖于固定的网络参数是否符合我们测试集的分布了。如果网络并没有训练好，会导致很多问题，所以引入了TTA作为一个更新方法。伪代码如下：

$\textbf{Algorithm:}$Test-Time Adaption Inference Algorithm
$\textbf{Input:}$ 目标模型 $\chi$ $\textbf{Output:}$ 形状编码$\hat{\phi}$, 关节角度$\hat{\psi}$，更新后的编码器参数$\hat{f_s}$ 1: 初始化$\phi\sim N(0,\sigma), \psi$ 2: $\_, \hat{\psi}=\arg\min_{\phi,\psi}L(\chi, \phi, \psi)$ //此处估计出了关节角度 3: $\hat{\phi}=\arg\min_{\phi}L(\chi,\phi,\hat{\psi})$ //代入估计出的关节角度，重新估计我们的形状编码 4: $\hat{f}_s=\arg\min_{f_s}L(\chi,\hat{\phi}, \hat{\psi})$ //TTA更新

​ 上述其实就是说，对于每一类，由于提出的shape-encoder有类间的共享的feature，所以可以通过额外观测的测试集数据继续调整学习到的分布。

​ 这个算法其实有点模糊了训练和测试的边界，不知道这种思路是否是通用的。

Articulated Shape Synthesis

​ 当我们有了形状参数以后，我们就可以合成没有见过的角度的实例。可以看做一个生成式网络。比起变分推断的input是高斯分布的采样，这里是把分布align到了joint range上来创建，然后创建的方式是基于sample的inference得到SDF value来创建整个模型。相对传统的网络我觉得还是比较新颖的。

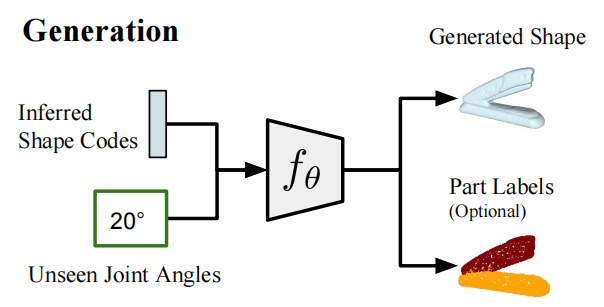
实验

实验部分略，等到有需要再看。不过值得一提的是，TTA在现实中的深度图上测试时效果很好，因为TTA意味着使用训练集分布作为初始值，在测试集上继续拟合其分布，所以可以克服一定的sim2real gap。