(IJCAI2018)Behavior Clone from Observation

​ 通过这篇论文继续补充自己的理论知识。

​ 在智能体通过模仿others的任务完成过程从而进行模仿学习的时候，通常会遇到两个问题：

• 通常模仿的内容（示教）只有状态信息而没有显式的动作信息。
• 学习速度要非常快。

​ 这篇工作提出了一个2阶段的自动模仿学习技术，叫做behavior cloning from observation。

模仿学习

​ 本图来源于OpenDeepRL，是对模仿学习的系统解构，这样我们就知道了其实我们上次所看到的SOIL和本篇文章的BCO都是基于反向动态模型(inverse dynamics model)的模仿学习策略，看来要把整个领域完全涵盖还是需要很大功夫的，包括说手头上的代码能力也需要同步提升起来。

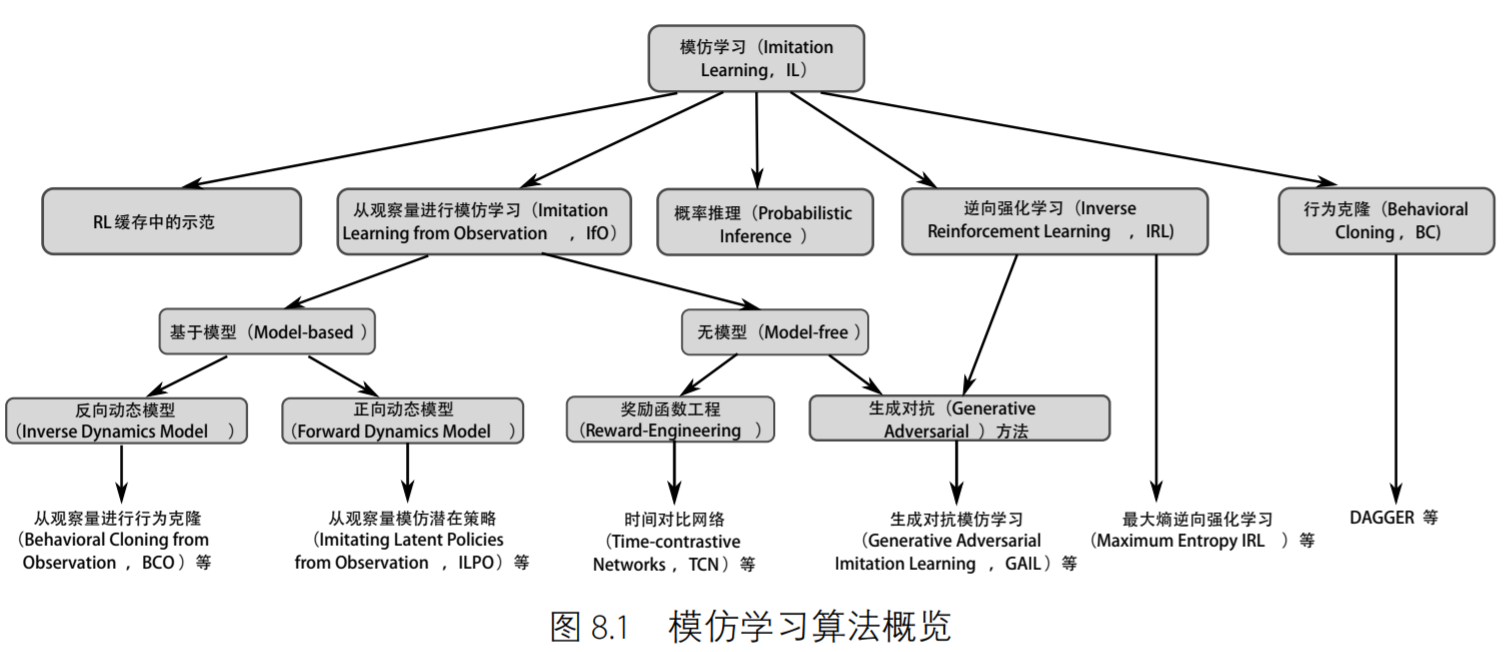
行为克隆(Behavior Clone)

​ 这篇文章是搜Behavior Clone偶然搜到的高引，但由上图可知，其实BCO和BC并不属于同一个模仿学习分支，故此处先摘抄深度强化学习中对BC的定义。使用监督学习模仿专家示范的方法在文献中称为$\textbf{行为克隆}$。

​ 给定示教数据集$D=\{(s_i,a_i)|i=1,…,N\}$，我们可以训练出确定性的专家策略$\pi_{\theta}(s)$，优化目标如下：
$$
\min_{\theta}\sum_{(s_i,a_i)\sim D}||a_i-\pi_\theta(s_i)||_2^2
$$
​ 一些随机性策略$\pi_{\theta}(\widetilde{a}|s)$的具体形式，如高斯策略等，可以通过再参数化技巧来处理：
$$
\min_{\theta}\sum_{\widetilde{a}_i\sim\pi(\cdot|s_i),(s_i,a_i)\sim D}||a_i,\widetilde{a}_i||_2^2
$$

问题重述

​ 马尔科夫决策过程（MDP）通过五元组$M=\{S,A,T,r,\gamma\}$表述，其中S是状态空间，A是动作空间，$T_{s_{i+1}}^{s_i,a}=P(s_{i+1}|s_i,a)$代表了智能体在状态$s_i$下执行动作$a$转移到状态$s_{i+1}$的概率，$r:S\times A\rightarrow R$是描述立即奖励的函数，$\gamma$是打折因子。智能体的行为为$\pi: S\rightarrow A$。一个智能体以策略$\pi$所经历的一系列状态转换，在本文中用$T_{\pi}=\{(s_i,s_{i+1})\}$来表示。

​ 在这些转换中，我们关心的是反向动态模型。也就是我们仅仅能知道状态转移$(s_i,s_{i+1})$的时候，我们希望得到对应的$a_i$的概率分布。

​ 我们继续把 state 划分为智能体特定的 state $S^a$和任务特定的 state $S^t$，即$S=S^a\times S^t$。在这个划分下，我们定义智能体特定的 反向动态模型为$M_{\theta}: S^a\times S^a\rightarrow p(A)$，它把 $(s_i^a,s_{i+1}^a)\in T_{\pi}^a$ 映射到对应的动作分布上。

​ 模仿学习通常定义在没有显式 reward function 的MDP上，即 $M$\ $r$。智能体目标就是学习像专家一样的策略$\pi:S\rightarrow A$，智能体有的可以学习的东西就是专家的示教集合，即$\{\xi_1,\xi_2,…\}$，其中每个$\xi$是一条示教轨迹$\{(s_0,a_0),(s_1,a_1),…,(s_N,a_N)\}$。因此，智能体必须要得到示教集中的动作才能去学习。对于示教轨迹没有动作的情况，这就是一个从观察中进行模仿学习（Ifo）的场景。

本文中的问题定义

​ 给定一系列只包含状态的示教轨迹$D$，使用最小的post-demonstration环境交互$|I^{post}|$来找到一个好的模仿学习策略。

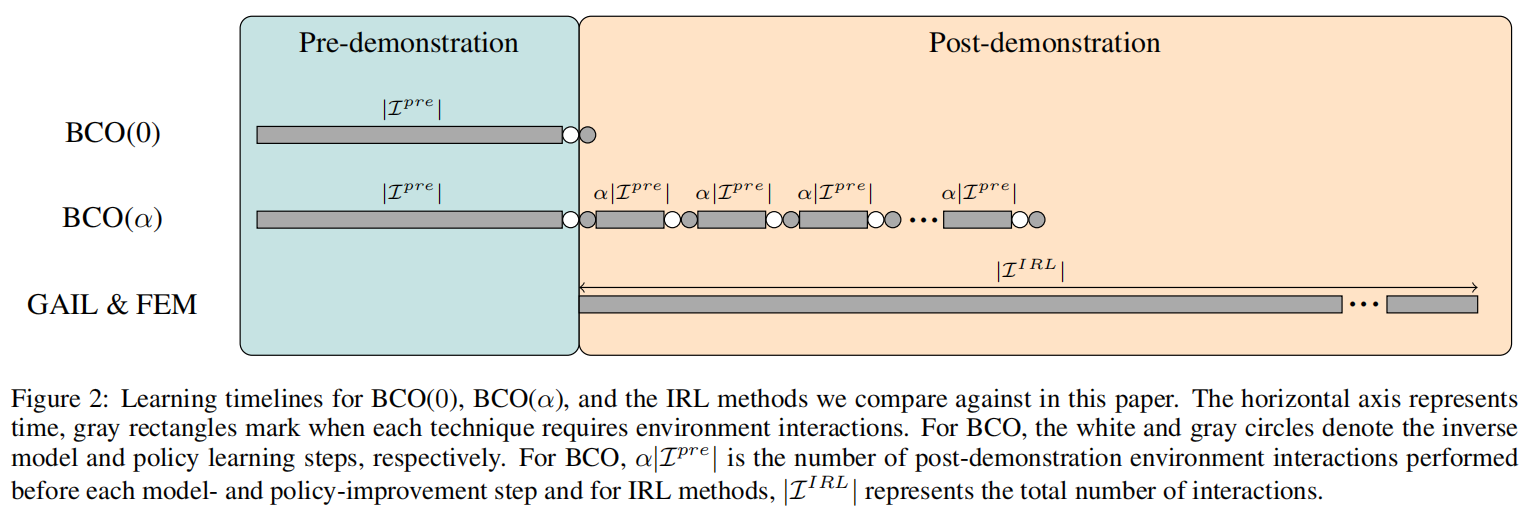
BCO(0)

​ 本文提出了两个基础模块：inverse dynamics model和behavior cloning模块。

反向动态模型(Inverse Dynamics Model)

​ 我们可以让智能体使用随机策略$\pi$收集一些先验的经验，记为$I^{pre}$。我们把反向动态模型用参数$\theta$描述为$M_{\theta}$。在这一阶段，我们简单地使用极大似然估计来得到$\theta^*$，即：
$$
\theta^*=\arg\max_{\theta}\prod_{i=0}^{|I_{pre}|}p_{\theta}(a_i|, s_i^a,s_{i+1}^a)
$$
​ 其中$p_\theta$是模型$M_\theta$对于一个转移所估计出来的可能动作的分布。对于这个模型，我们使用随机梯度下降来进行训练。也就是当我们有样本$(s_{i},a_{i},s_{i+1})$的时候，我们会让梯度的目标为提高对应$a_i$的概率。

Behavior Cloning

​ 我们从示教集合$D_{demo}$中提取出agent-specific的状态转移对，构成$T_{demo}^a=\{(s_t^a,s_{t+1}^a)\}$，并且使用我们刚才先验训练好的模型$M_{\theta^*}$估计出$\widetilde{a}_i$，这样我们就有了有对应估计出的动作的示教数据集。有了这个以后，我们就可以尝试对模仿策略$\pi_\phi$做估计了，也就是找到一个参数$\phi$，使得产生出含估计动作的示教数据集的概率最大，也是极大似然估计的思想：
$$
\phi^*=\arg\max_{\phi}\prod_{i=0}^N\pi_{\phi}(\widetilde{a}_i|s_i)
$$
​ 我们使用神经网络把策略参数$\phi^*$给学出来。

BCO($\alpha$)算法

​ 上述两个描述了BCO算法的基本模块。如果我们希望进一步从后验的环境交互中进一步提升我们的两个模型的话，本文提出了叫做$BCO(\alpha)$的改进版本，它可以同时提升学习到的inverse dynamics模型和最终估计出来的模仿策略。

​ 在每一步behavioral cloning后，智能体可以在环境中执行它所估计出来的imitation policy一段时间。然后，我们收集新的state-action序列来更新模型和对应的imitation policy。

​

BCO($\alpha$)算法
用随机参数来初始化$M_{\theta}$ 用随机参数来初始化$\pi_{\phi}$ 设置$I=

​ 其中的$\alpha$是用来控制pose-demonstration环境交互和pre-demonstration的比例，当我们指定非零的$\alpha$的时候，我们就可以迭代地改进我们的反向动态模型和学习到的imitation policy。

实验

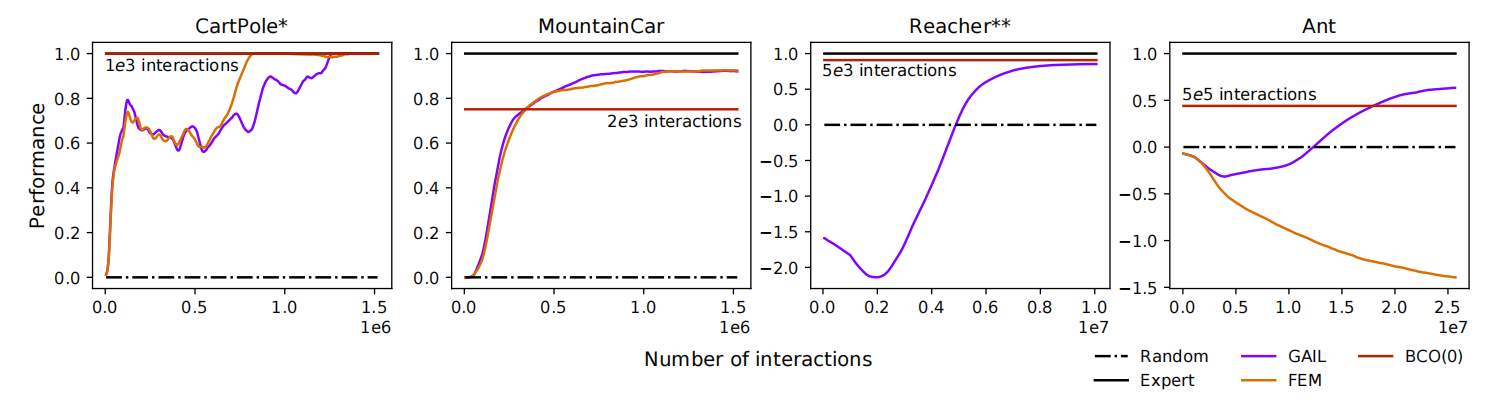
​ 其中的GAIL和FEM都是IRL的baseline，注意到因为我们在训练之前已经收集并且训练了pre-demonstration experience并且训练完了反向动态模型，所以我们最终的BCO(0)的动作是固定的反向动态模型所输出的模型。

​ 具体细节等到需要了再回来看。

比较一下SOIL和这篇文章

​ 因为SOIL提到了behavior cloning，所以搜到了这篇文章，并且看下来感觉两篇文章还挺像的，所以还是对比一下两者。

更新模型的角度

​ SOIL使用了改进的模仿学习策略梯度，有一个模仿学习项来更新策略，即
$$
g_{soil}=g+\lambda_0\lambda_1^k\sum_{(s,a’)\in D’}\nabla_{\theta}\log\pi_{\theta}(a’|s)
$$
​ 而这篇文章只是简单地用神经网络做了极大似然估计尝试把策略的概率分布估计出来。

算法的角度

​ 在$BCO(0)$中，因为它pre-demonstration使用的是随机策略，如果动作空间维度很大，那么可能根本学不到一个好的inverse dynamics模型，所以基本上$BCO(\alpha)$是标配。$BCO(\alpha)$和SOIL的区别其实不大，感觉SOIL只是在灵巧手这个特定的角度切入去做了一个work的工作，所以从创新性来说，SOIL最终投到了IROS是合理的。